
 Voriges Unterkapitel 3.4
Voriges Unterkapitel 3.4
 Nächstes Unterkapitel 3.6
Nächstes Unterkapitel 3.6
 Einleitung
Einleitung
 Experimentelle Ökonomie
Experimentelle Ökonomie
 Austrian Political Stock Market
Austrian Political Stock Market
 Literaturverzeichnis
Literaturverzeichnis
 Inhaltsverzeichnis
Inhaltsverzeichnis
 Zur ASPM-Homepage
Zur ASPM-Homepage
| Ergebnis | APSM | |
| 28.11.94 | ||
| SPÖ-Alleinregierung | - | 0,000 |
| ÖVP-Alleinregierung | - | 0,001 |
| Große Koalition | realisiert | 9,997 |
| Kl. Koalition mit SPÖ | - | 0,010 |
| Kl. Koalition mit ÖVP | - | 0,010 |
| Andere Regierungsform | - | 0,010 |
In der obigen Tabelle ist das Endergebnis dieses Marktes wiedergegeben. In der Spalte APSM sind die Kurse der letzten durchgeführten Transaktionen der einzelnen Aktien angeführt. Dieser Markt wurde gemeinsam mit den anderen beiden Märkten EU-Volksabstimmung und Nationalratswahlen gestartet. Er unterscheidet sich von den übrigen beiden dadurch, daß am Ende für jene Aktie der gesamte Bündelpreis von ATS 10,00 ausbezahlt wird, welche der realisierten Regierungsform entspricht. Alle übrigen Aktien sind dadurch am Ende wertlos. Märkte mit einer solchen Auszahlungsregel werden als ein "Winner takes all"-Markt bezeichnet. In diesem speziellen Fall bestand keine Möglichkeit, eine andere Auszahlungsregel zu verwenden, da es in einem bestimmten Zeitraum ja nur eine Regierungsform geben kann.
Im Gegensatz zu den anderen beiden Märkten wird das Ergebnis nicht durch eine Abstimmung oder durch eine Wahl bestimmt, sondern durch Verhandlungen. In der Meinungsforschung wird deshalb ein relativ geringes Gewicht auf diese Fragestellung gelegt; so konnten nur vereinzelt Umfragen gefunden werden, die sich mit diesem Thema befassen. Die Ergebnisse dieser Untersuchungen sind darüberhinaus mit dem APSM-Markt Regierungsform nicht vergleichbar, da die Fragestellungen unterschiedlich sind: Meinungsforscher stellen die Frage, welche Regierungsform dem Wähler am liebsten wäre; im APSM-Markt geht es aber um die Frage, welche Regierungsform am wahrscheinlichsten realisiert wird.
Das Ergebnis dieses Marktes war von Anfang an ziemlich klar. Ein Fortsetzen der Großen Koalition von SPÖ und ÖVP war immer die plausibelste Alternative. Dennoch ist eine genauere Betrachtung der Kursverläufe von Interesse. So sei vor allem auf die Entwicklung der Gr. Koalition-Aktie hingewiesen, welche anfangs zu ATS 8,00 gehandelt wurde und im Laufe der Zeit auf fast ATS 10,00 kletterte.
Abbildung 52: Kursdiagramm aller Aktien des Marktes Regierungsform
Die SPÖ ist seit Jahrzehnten die größte Partei. Die Zeiten, in denen eine Partei die absolute Mehrheit inne hat, sind aber in Österreich vorbei. In den letzten Jahren verloren alle beiden Großparteien, sei es nun die SPÖ, wie auch die ÖVP, kontinuierlich Wähler an die kleineren Parteien. Von diesem Verlust profitierte in den letzten Jahren vor allem die FPÖ, und bei diesen Wahlen auch LF und Grüne. Gründe für den Wählerverlust der Großparteien ist das Verschwinden der Stammwählerschaft. Durch die Austragung des Wahlkampfes in den Medien sind Inhalte meist weniger wichtig als eine charismatische Persönlichkeit.
Dies sind einige Gründe, die eine SPÖ-Alleinregierung nicht sehr wahrscheinlich machten. Der Kurs dieser Aktie bewegte sich bei den meisten Transktionen unter 0,50%. Nach den Nationalratswahlen wurde diese Aktie knapp über Null Schilling gehandelt und am 17.11.1994 fand die letzte Transaktion dieser Aktie bei einem Kurs von ATS 0,00 statt.
Überraschend finde ich es dennoch, daß diese Aktie überhaupt gehandelt wurde. Wie oben gesehen, sprechen die fundamentalen Daten ganz entscheidend gegen einen Kauf dieser Aktie. Der Anreiz mit dieser Aktie zu handeln, scheint aber vor allem der geringe Preis in Kombination mit einer im Vergleich zum Einsatz hoher Gewinnaussicht zu sein.
Abbildung 53: Börsendiagramm der SPÖ-Alleinregierung-Aktie
Abbildung 54: Börsendiagramm mit gleitenden Durchschnittskurven der SPÖ-Alleinregierung-Aktie
Abbildung 55: Eingegebene limitierte Kauf- und Verkauforder der SPÖ-Alleinregierung-Aktie (nicht verfügbar)
Abbildung 56: Alle Transaktionen der SPÖ-Alleinregierung-Aktie
Abbildung 57: Zeitlich verzerrter Kurs der -Aktie
Ähnlich wie bei der Analyse der SPÖ-Alleinregierungs-Aktie ist die Möglichkeit einer ÖVP-Alleinregierung nur theoretischer Natur. Diese Möglichkeit würde eine Minderheitsregierung mit stiller Unterstützung einer oder mehrerer kleiner Parteien bedeuten. Vor den Nationalratswahlen sprach niemand von dieser Variante, sodaß die Kurse erwartungsgemäß sehr niedrig waren. Die meisten Transaktionen kamen bei einem Kurs von unter 0,20% zustande. Nach den Nationalratswahlen brach der Kurs, ähnlich wie bei der SPÖ-Alleinregierung, dann gänzlich zusammen.
Bei der Analyse der Kursverläufe ist besonders in diesem Markt darauf zu achten, diese nicht isoliert zu betrachten. Hauptsächlich ist die Konstruktion des APSM als Nullsummenspiel dafür verantwortlich: das Steigen einer Aktie ist nur durch das Fallen einer oder mehrerer anderer Aktien möglich. Ein Steigen der ÖVP-Alleinregierung-Aktie würde somit nur dann erfolgen, wenn gleichzeitig der Kurs einer oder mehrerer anderer Aktien fallen würde. Theoretisch würde das heißen, daß die Summe aller Kurse eines Marktes zu jeder Zeit dem Bündelpreis entsprechen müßte. In der Praxis zeigt sich aber, daß diese Summe in den wenigsten Fällen genau diesem Wert entspricht. Solche Abweichungen halten sich aber in Grenzen, sodaß die obige Regel nichts von ihrer Aussagekraft verliert.
Abbildung 58: Börsendiagramm der ÖVP-Alleinregierung-Aktie
Abbildung 59: Börsendiagramm mit gleitenden Durchschnittskurven der ÖVP-Alleinregierung-Aktie
Abbildung 60: Eingegebene limitierte Kauf- und Verkauforder der ÖVP-Alleinregierung-Aktie (nicht verfügbar)
Abbildung 61: Alle Transaktionen der ÖVP-Alleinregierung-Aktie
Abbildung 62: Zeitlich verzerrter Kurs der ÖVP-Alleinregierung-Aktie
Abbildung 63: Performance SPÖ-Aktie, ÖVP-Aktie, Große Koalition-Aktie (nicht verfügbar)
Die obige Abbildung zeigt die Performance der SPÖ-Aktie, der ÖVP-Aktie sowie der Gr. Koalition-Aktie. Ein Zusammenhang in der Entwicklung der Kursverläufe von SPÖ- und ÖVP-Aktie einerseits und Gr. Koalition-Aktie andererseits ist nicht ersichtlich. Ganz deutlich sieht man allerdings einen Zusammenhang zwischen SPÖ-Aktie und ÖVP-Aktie. Der Kurs der Gr. Koaltion-Aktie ist gekennzeichnet durch einem rasanten Aufwärtstrend in den ersten Wochen nach Marktöffnung, welcher bis einen Tag vor der EU-Volksabstimmung dauert. An diesem Tag ist eine starke Nervosität bei den Händlern bemerkbar: die Kurse der einzelnen Transaktionen schwanken ziemlich stark. In den ersten drei Tagen nach der Volksabstimmung erreicht diese Aktie fast den Maximalwert von ATS 10,00. Diese plötzliche Reaktion könnte auf die Aussage der ÖVP und SPÖ zurückzuführen sein, welche gleich nach dem Bekanntwerden des Abstimmungsergebnisses eine Fortführung der Großen Koaltion ankündigten. Ausgehend vom Kursnievau vor der Volksabstimmung ist ein deutlicher Aufwärtstrend zu erkennen, welcher erst Anfang Juli gestoppt wird. In den Monaten Juli, August und September kommen die Umsätze fast zum Erliegen, was auf die Sommerferien zurückzuführen ist. Knapp vor den Nationalratswahlen am 9.10.1994 liegt der Kurs bei ungefähr ATS 9,40. Verschiedene Diskussionen in den Medien über mögliche Alternativen zur Gr. Koalition lassen den Kurs der Gr. Koalition-Aktie etwas fallen. Nach den Nationalratswahlen steigt der Kurs dann innerhalb von ca. 2 Wochen auf knapp ATS 10,00 und verbleibt dort bis zur Bekanntgabe der neuen Regierung Ende November 1994.
Abbildung 64: Börsendiagramm der Große-Koaltion-Aktie
Abbildung 65: Börsendiagramm mit gleitenden Durchschnittskurven der Große-Koaltion-Aktie
Abbildung 66: Eingegebene limitierte Kauf- und Verkauforder der Große-Koaltion-Aktie (nicht verfügbar)
Abbildung 67: Alle Transaktionen der Große-Koaltion-Aktie
Abbildung 68: Zeitlich verzerrter Kurs der Große-Koaltion-Aktie
Der Kurs dieser Aktie bewegte sich im Zeitraum von der EU-Volksabstimmung bis vor die Nationalratswahlen immer auf einem niedrigen Niveau von ungefähr 3%. Vor der Volksabstimmung lag der Kurs bei ungefähr 4% und darüber; nach den Nationalratswahlen brach der Kurs zusammen, wobei die Aktie den gesamten Kurswert verlor. Diesen Kursverlauf sieht man am besten in Abbildung 72.
Abbildung 69: Börsendiagramm der Kl. Koaltion mit SPÖ-Aktie
Abbildung 70: Börsendiagramm mit gleitenden Durchschnittskurven der Kl. Koaltion mit SPÖ-Aktie
Abbildung 71: Eingegebene limitierte Kauf- und Verkauforder der Kl. Koaltion mit SPÖ-Aktie (nicht verfügbar)
Abbildung 72: Alle Transaktionen der Kl. Koaltion mit SPÖ-Aktie
Abbildung 73: Zeitlich verzerrter Kurs der Kl. Koaltion mit SPÖ -Aktie
Abbildung 74: Performance ÖVP-Aktie, FPÖ-Aktie und Kl. Koalition ÖVP-Aktie (nicht verfügbar)
Die Aktie Kl. Koalition mit ÖVP wurde deshalb mit der ÖVP- und FPÖ-Aktie verglichen, da es immer wieder Anzeichen für eine mögliche Zusammenarbeit von ÖVP und FPÖ gab. Dies könnte eine Erklärung für das Ansteigen des Kurses der Kl. Koalition-Aktie kurz vor den Nationalratswahlen sein. In der obigen Abbildung sieht man eine deutliche Spitze der FPÖ-Performance, genau in dem Zeitraum, in dem auch die Performance der Kl. Koalition mit ÖVP-Aktie einen starken Zuwachs verzeichnet. Dieses Hoch ist aber nur von kurzer Dauer, und deshalb eher auf Spekulation zurückzuführen. Interessant ist auch eine kurze Spitze vor der EU-Volksabstimmung, gefolgt von einem deutlichen Absinken auf ein niedrigeres Niveau, welches dann bis kurz vor den Nationalratswahlen gehalten wird.
Abbildung 75: Börsendiagramm der Kl. Koaltion mit ÖVP-Aktie
Abbildung 76: Börsendiagramm mit gleitenden Durchschnittskurven der Kl. Koaltion mit ÖVP-Aktie
Abbildung 77: Eingegebene limitierte Kauf- und Verkauforder der Kl. Koaltion mit ÖVP-Aktie (nicht verfügbar)
Abbildung 78: Alle Transaktionen der Kl. Koaltion mit ÖVP-Aktie
Abbildung 79: Zeitlich verzerrter Kurs der Kl. Koaltion mit ÖVP-Aktie
Diese Aktie schließt alle Regierungsformen ein, welche nicht durch die übrigen Alternativen in diesem Markt abgedeckt werden. Eine "Andere" Regierungsform, wäre z.B. eine Koalition aus SPÖ, ÖVP und LF. Eine solche Möglichkeit wurde in den Tagesnachrichten öfters diskutiert: rechnerisch wäre eine Zusammenarbeit von SPÖ, ÖVP und LF eine denkbare Alternative gewesen. Zu sehr waren allerdings sowohl die Grünen als auch das LF auf ihre Rolle als Opposition bedacht, sodaß eine ersthafte Diskussion einer solchen Alternative eigentlich nie stattgefunden hat.
Der Kursverlauf ist wegen der obigen Gründe sehr niedrig; bei den meisten Transaktionen liegt der Kurs unter ATS 0,10, was einer Realisationswahrscheinlichkeit von weniger als 1% entspricht. Auffallend ist der Kursverlauf vor allem in den Sommermonaten, in denen der Kurs beträchtlich schwankt. Bei Marktschluß betrug der letzte Kurs, zu dem diese Aktie gehandelt wurde, ATS 0,01. Ähnlich wie bei anderen "kleinen" Aktien im APSM ist es auch hier nicht möglich, Kursschwankungen mit bestimmten Ereignissen in Verbindung zu bringen. Für die Kursschwankungen im Sommer dürfte deshalb vor allem das Fehlen einer beträchlichen Anzahl von Händlern verantwortlich gewesen sein. Eben dieses bewirkt, daß Kursausbrüche und Schwankungen mit besonderer Vorsicht zu interpretiern sind. Dies entspricht der Faustregel auf Aktienmärkten, daß zum einen ein hohes Handelsvolumen die Bewegungsrichtung eines Kurses bestätigt, und zum anderen Kursschwankungen auf engen Märkten i.a. viel schwieriger zu interpretieren sind.
Abbildung 80: Börsendiagramm der Andere-Regierungsform-Aktie
Abbildung 81: Börsendiagramm mit gleitenden Durchschnittskurven der Andere-Regierungsform-Aktie
Abbildung 82: Eingegebene limitierte Kauf- und Verkauforder der Andere-Regierungsform-Aktie (nicht verfügbar)
Abbildung 83: Alle Transaktionen der Andere-Regierungsform-Aktie
Abbildung 84: Zeitlich verzerrter Kurs der Andere-Regierungsform-Aktie
Nichtlineare Modelle, populär geworden als chaotische Systeme (Apfelmännchen), finden in zunehmendem Maße Anwendung in technisch und wirtschaftlichen Bereichen. Unter Chaos werden nichtlineare deterministische Prozesse verstanden, die aussehen, als ob sie zufällig wären [Hsieh 1991] S.1840. So gibt es auch in der Finanzwirtschaft zahlreiche Ansätze, die versuchen für verschiedene reale Gegebenheiten nichlineare Modelle zu bilden (32).
Solche Modelle werden i.a. durch ein Differenzen- oder ein Differentialgleichungssystem beschrieben. Ohne auf einzelne Details näher einzugehen seien die wichtigsten Charakteristika nichtlinearer dynamischer Systeme kurz erwähnt:
Die obigen ersten zwei Punkte sagen nichts anderes aus, als daß der Funktionswert xt in einer nichtlinearen Abhängigkeit von den Werten xt-i steht. Ist der Wert xt nur von xt-1 abhängig, so ist der Maximalwert des Index i eins, und das Chaotische System füllt den Eindimensionalen Raum, d.h. eine Linie, aus. Untersuche ich ein solches System, so kann ich zwar den Verlauf der Linie bestimmen, nicht aber den Punkt auf dieser Linie, der nach einigen Iterationen beschrieben wird. Wichtig scheint es auch zu erwähnen, daß durch die Nichtlinearität große Sprünge erklärt werden können.
Um die Relevanz von chaotischen Systemen bei der Analyse eines politischen Aktienmarktes zu zeigen, müssen zwei unterschiedliche Ansätze zur Beschreibung von wirtschaftlichen Entwicklungen näher betrachtet werden. Beim ersteren nimmt man an, daß das Wirtschaftssystem, bzw. die Aktienkurse im Gleichgewicht sind und die Kursänderungen durch äußere Einflüsse (siehe 3.2.1 News-Days) hervorgerufen werden (Box-Jenkins-time-series-models). Der zweite Ansatz hingegen geht davon aus, daß das Wirtschaftsystem den Prinzipien eines nichtlinearen dynamischen Systems folgt, wodurch scheinbar zufällige Sprünge (endogen) erklärt werden können. Was für den zweiten Ansatz spricht, ist die Tatsache, daß z.B. Aktienkurse immer wieder (große) Sprünge vollziehen, für die Erklärungen auf der Basis von "News" fehlen. Ein gutes Beispiel für einen solchen Kurssprung ist der Börsencrash am 19. Oktober 1987.
Für beide Ansätze können Argumente dafür und dagegen gefunden werden, wobei ein endgültiges Ergebnis weder existiert, noch existieren muß. Ich teile die Ansicht verschiedener Forscher, wonach immer nur für ein konkretes (reales) System in einem bestimmten Zeitabschnitt entschieden werden, nach welchen Mustern sich dieses verhält.
Nichtlineare dynamische Modelle werden i.a. durch Differenzen- bzw. Differentialgleichungen beschrieben. Durch eine solche Beschreibung ist es im allgemeinen möglich festzustellen, für welche Parameterwerte dieses System einen Gleichgewichtszustand erreicht und wann nicht. Für reale Systeme ist es ungleich schwieriger zu entscheiden, ob es sich tatsächlich um ein chaotisches System handelt. Grassberger und Procaccia [Hsieh 1991] S.1845 entwickelten ein Verfahren zur Identifikation von chaotischen Systemen. Dieses Verfahren untersucht, bis zu welcher Dimension die Daten eines Systems einen N-dimensionalen Raum ausfüllen und bestimmt für jedes chaotische System einen Wert (correlation dimension). Für chaotische Systeme ist dieser Wert jeweils konstant, für zufällige Daten geht dieser Wert gegen unendlich.
Diese Vorgehensweise bietet den Vorteil, daß das Problem der Darstellung von einem N-dimensionalen Raum umgangen wird. Der Ansatz, der in diesem Kapitel gemacht wird, verwendet hingegen eine Projektion eines N-Dimensionalen Raumes auf eine zweidimensionale Fläche.
Das Tool, das hierfür benötigt wird, ist ein neuronales Netz nach dem Modell von Kohonen (33). Die Fähigkeit dieses Modells besteht darin, ohne a-priori-Informationen - aufgrund einfacher Selbstorganisationsregeln - eine nichtlineare Abbildung eines (N-Dimensionalen) Raumes der Eingangssignale auf eine zweidimensionale Neuronenschicht zu leisten [aus Kapitel 6.1 Selbstorganisierende Karten]. Dieses neuronale Netz kann dazu verwendet werden, Objekte mit verschiedenen Eigenschaften zu gruppieren, ohne vorher festlegen zu müssen, wieviele Gruppen es geben soll bzw. wie solche Gruppen überhaupt aussehen sollen. Vom Konzept her handelt es sich um das aus anderen Bereichen bekannte Clustering. Der Vorteil des neuronalen Netzes liegt dabei in der graphischen Darstellung. Als klassisches Beispiel soll hier die Klassifikation von Tieren beschrieben werden. Tiere können als Objekte mit verschiedenen Eigenschaften angesehen werden. Ein Löwe ist z.B. ein Raubtier, geht auf vier Beinen, ist ein Säugetier; bestimmte andere Eigenschaften besitzt er hingegen nicht. Das Ergebnis des Neuronalen Netzes ist nun eine (zweidimensionale) Karte, wobei ähnliche Tiere sehr nahe beieinander liegen und unähnliche weit auseinander. Diese Aufteilung erfolgt ohne Rückkopplung d.h. ohne zusätzliche Eingaben des Benutzers. Es erfolgt somit eine Projektion des n-dimensionalen (Eigenschafts-)Raumes auf eine zweidimensionale Fläche. Von der Struktur her wird dadurch ein ähnliches Ergebnis wie jenes von Grassberger und Procaccia erreicht. Sollte es sich bei den Daten um Zufallszahlen handeln, so sind die einzelnen Datenwerte über die gesamte Fläche der selbstorganisierenden Karte verteilt. Beinhalten die Daten hingegen irgendwelche Abhängigkeiten, wobei diese Korrelation nun linear oder nichtlinear sein kann, so liegen diese Daten auf der selbstorganisierenden Karte in mehr oder weniger klar abgegrenzten Flächen gruppiert.
Nun bietet sich dieses Modell förmlich für die Anwendung zur Analyse der APSM-Daten an. Es muß allerdings vorweggenommen werden, daß bestenfalls qualitative Ergebnisse, nie aber quantitative Ergebnisse erziehlt werden können. Diese Tatsache mußten auch jene Forscher zur Kenntnis nehmen, die versuchten auf der Grundlage von neuronalen Netzen Prognosen für zukünftige Aktienverläufe zu erstellen.
Um die Brauchbarkeit des neuronalen Netzes für diese Aufgabe zu testen, wurden die Daten eines einfachen bekannten chaotischen Systems analysiert: der Logistik-Map (34).
Die mathematische Formulierung der Logistik-Map erfolgt in Form folgender Differenzengleichung:
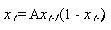
Wie man sieht ist der Wert zum Zeitpunkt t durch die Kenntnis des Wertes zum Zeitpunkt t-1 eindeutig bestimmt. xt liegt zwischen 0 und 1; der Parameter A liegt zwischen 0 und 4. Nähert sich der Parameter dem Wert 4, so verhält sich diese System chaotisch.
Dieses System ist deshalb gut für diesen Zweck geeignet, da die Daten dieses Systems einen eindimensionalen Raum ausfüllen, also eine Linie bilden. Ausgehend von den generierten Daten wurden jeweils N hintereinanderliegende Daten zu einer Gruppe zusammengefaßt; diese Gruppen überlappen sich gegenseitig. Eine Gruppe, oder vielleicht besser jeder Datenvektor besteht aus N im Zeitablauf hintereinander liegenden Kursen.
Aus der (Beispiel-) Datenreihe: (1,4,3,2,7,8,8,3,6,5,7, ... )
würden die folgenden Datenvektoren generiert
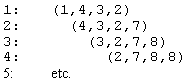
Jeder Datenvektor besteht aus gleichvielen Elementen; durch diese Anzahl M wird die höchste identifizierbare Dimension (M-1) des untersuchten nichtlinearen determinitstischen Systems festgelegt. Bei Datenvektoren mit jeweils 4 Elementen würde das heißen, daß ich davon ausgehe, daß der Funktionswert zum Zeitpunkt t höchstens noch vom Wert zum Zeitpunkt t-3 abhängt und ich damit von einem dreidimensionalen chaotischen System ausgehe. Alle Werte, welche weiter als t-3 in der Vergangenheit liegen, sind für den Wert zum Zeitpunkt t nicht relevant. Bei einer Datenreihe, welche aus den Kursen einer Aktie gebildet wurde, würde dies bedeuten, daß der Kurs an einem bestimmten Tag von den Kursen der letzten Woche, des letzten Jahres, oder irgend eines anderen Zeitraumes, abhängen. Anders betrachtet würde dies auch heißen, daß der heutige Kurs, bei einer nichtlinearen Abhängigkeit von einer Woche, unabhängig ist von allen Kursen die vor einer Woche gebildet wurden. Geht man nun einen Schritt weiter und nimmt an, daß der gestrige Kurs einen stärkeren Einfluß auf den Kurs von heute ausübt, als der Kurs von vorgestern, so kann man den Aktienkurs als Information interpretieren, welche mit der Zeit an Wert verliert und irgendwann wertlos ist.
Bei der Untersuchung der Daten der Logistik Map wurden zum Vergleich Zufallsdaten generiert, die ebenfalls zu Gruppen zusammengefaßt wurden. Dies war deshalb notwendig, da ansonsten nur Abhängigkeiten innerhalb der Daten gefunden würden. Eine solche Vorgangsweise entspricht dem Test einer Untersuchungsmethode mit zwei getrennten Versuchen. Beide Versuche unterscheiden sich nur aufgrund einer vorher festgelegten Eigenschaft. Sind die Ergebnisse bei beiden Versuchen verschieden, so kann davon ausgegangen werden, daß die Untersuchungsmethode zur Erkennung dieser Eigenschaft geeignet ist. In unserem Fall heißt das, daß ein Datenreihe mit zufälligen Werten einer Datenreihe mit zeitlich voneinander abhängigen Werten gegenübergestellt wird.
Das neuronale Netz wurde nun sowohl mit den aus den Zufallszahlen generierten Vektoren als auch mit den Vektoren der Logistik-Map trainiert. Zur Unterscheidung wurden jeweils verschiedene Symbole verwendet. Das Ergebnis war verblüffend. Das neuronale Netz zeichnete die Punkte der Vektoren des chaotischen Systems (Kreuze) genau in einer Linie, wohingegen die Punkte der Vektoren der Zufallszahlen (Kreise) wild über den Bildschirm verstreut waren. Das Ergebnis war dabei unabhängig von der Anzahl der in einer Gruppe zusammengefaßten Werte (!).
Abbildung 85: Graphische Darstellung der Logistik Map
Abbildung 87: Analyse der FPÖ-Kurse mit einer selbstorganisierenden Karte
Nun wurde dieselbe Vorgangsweise für die Kurse des APSM angewandt. Das Ergebnis ist hier schwieriger zu interpretieren. Ganz deutlich tritt hier das Problem auf, daß jedes nichtlineare System mit mehr als 2 Dimensioen bei der Abbildung auf eine zweidimensionale Fläche eine Fläche ausfüllt. Für die Daten konnte eine Clusterung festgestellt werden; d.h. die Vektoren, gebildet aus den Daten des APSM waren näher beeinander als die Vektoren der Zufallsvariablen. Als allgemeines Ergebnis kann daraus abgeleitet werden, daß die Daten des APSM eher keine Zufallszahlen darstellen. Es kann allerdings nicht bestimmt werden, ob es sich tatsächlich um ein nichtlineares System handelt, oder ob die Zusammenhänge der einzelnen Kurse "nur" linearer Natur sind. Nur weitergehende statistische Untersuchungen können diese Fragen beantworten. Allerdings führen auch diese Methoden nicht zum gewünschten Ziel, da im APSM die Datenbasis dafür zu klein ist. Eine sehr gründliche Untersuchung der Kursverläufe an deutschen Aktienbörsen über einen Zeitraum von 30 Jahren konnte keinerlei statistisch signifikante nichtlineare Zusammenhänge in den Kursverläufen feststellen. Alle Zusammenhänge konnten entweder durch Autokorrelation, oder durch Heteroskedastik erklärt werden (35).
Neben dem Versuch Chaos in den Daten von Aktienkursen zu untersuchen gibt es daneben den Versuch mittels ganz konkreter nichtlinearer Gleichungssysteme das Verhalten von Aktienkursverläufen zu simulieren, um dadurch ein besseres Verständnis für reale Abläufe zu gewinnen, bzw. um Vorkommnisse wie etwa den Börsencrash 1987 erklären zu können. Im folgenden Kapitel wird ein solcher Ansatz kurz vorgestellt.
Friedrich Kugler [Kugler 1994] zeigt in seinem Buch "Preisbildung auf spekulativen Märkten" ein Modell eines Aktienmarktes, welches zwei besonders interessante Eigenschaften aufweist. Zum einen basiert das Modell auf 3 Differentialgleichungen, wodurch plötzliche Kurssprünge endogen erklärt werden können. Zum anderen findet eine ausführliche Diskussion der einzelnen Parameter statt, wobei hier wiederum sowohl auf die individuelle wie auch auf die kollektive Erwartungsbildung besonderes Gewicht gelegt wird, und der Autor im letzten Unterkapitel auf die Psychodynamik der Aktienkursbildung eingeht. Für die Analyse eines realen Aktienmarktes wie den APSM bietet dieses Modell all jene Verhaltensweisen, wie sie in der Realität auch anzutreffen sind. Ein noch komplizierteres Modell würde nur zu Lasten der Verständlichkeit gehen und somit keinen weiteren Vorteil bringen. Die nachfolgenden Ausführungen können nur einen kleinen Einblick in diese Arbeit bieten; für näheres zu diesem Thema sei unter anderem auf [Tvede 1991] und [Kugler 1994] verwiesen.
Die Modellgleichungen sehen folgendermaßen aus:
(1) 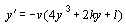
(2) 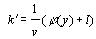
(3) 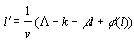 (36)
(36)
Prinzipiell modellieren diese 3 Gleichungen einen Aktienmarkt dessen Entwicklung sensitiv von der Abweichung des Ausgangskurses vom fundamentalen Wert, sowie vom Optimismus bzw. Pessimismus der Marktteilnehmer abhängt. Durch diese Kombination verschiedener Einfüsse auf das Händlerverhalten kann z.B. ein Price Bubble entstehen. Liegt der Wert einer Aktie über dem fundamentalen Wert und herrscht eine positive Stimmung unter den Händlern, so wird der Kurs weiter ansteigen, und zwar soweit, bis die Stimmung unter den Teilnehmern umkippt und daraufhin der Kurs wieder fällt. Wie bereits früher angesprochen kommt Smith [Smith 1988] in Laborexperimenten zu derselben Erklärung für das Entstehen und Platzen von Price Bubbles. Ansätze, die versuchen Price Bubbles auf realen Aktienmärkten zu identifizieren, führten bis zum heutigen Zeitpunkt zu keinen brauchbaren Ergebnissen. Dennoch können Price Bubbles auf realen Aktienmärkten nicht ausgeschlossen werden.
Im folgenden wird eine kurze Erklärung der einzelnen Parameter des obigen Differentialgleichungssystems gegeben. Gleichung (1) drückt die Anpassung der einzelnen Marktteilnehmer an die Mehrheit aus. Verhaltenswissenschaftlich kann diese Gleichung als der soziale Druck der "Masse" auf den Einzelnen interpretiert werden. Ein einzelner Trader ist dabei immer so klein, daß er sich früher oder später an die Meinung der Mehrheit anpaßt bzw. anpassen muß, will er im Markt verbleiben. Über den Parameter kann die Geschwindigkeit festgelegt werden, mit der sich die Broker auf eine neue Stimmungslage einstellen. Gleichung (2) gibt den Zweifel der Marktteilnehmer an, daß eine eingeschlagene Bewegungsrichtung (weg vom fundamentalen Wert) auch in Zukunft fortgesetzt wird. Je höher der Grad des Optimismus ist (l<0), umso mehr wächst auch der Zweifel, ob die optimistischen Erwartungen sich auch in der Zukunft erfüllen. Die Kursabweichung y geht über die Funktion (y) in k ein, wobei eine positive Abweichung vom Fundamentalwert (y>0) den Zweifel vermehrt, hingegen eine negative Kursabweichung (y<0) den Zweifel verringert. Der Parameter l´, der das Verhältnis von optimistisch zu pessimistisch eingestellten Händlern angibt, hängt erstens vom exogenen Parameter R ab, der die Grundstimmung am Aktienmarkt widerspiegelt; zweitens vom Zweifelsparameter k und drittens von der jeweils herrschenden Optimismus/Pessimismus-Situation (l).
Dieses Differentialgleichungssystem kann in Bezug auf Kursentwicklungen weitergehend interpretiert werden. Dazu stellen wir folgende Überlegung an. Zu einem bestimmten Zeitpunkt t stimmen die Erwartungen aller Teilnehmer überein; dies kann durch eine Normalverteilung modelliert werden. Nun wurde in der obigen Ausführung davon gesprochen, daß einige Händler zu der Überzeugung kommen, daß die Kurse nicht mehr dem bisher verfolgten Auf- bzw. Abwärtstrend folgen werden. Übernehmen andere Händler diese Meinung, so kommt es zu einem Meinunungsumschwung, der erst dann beendet ist, wenn alle Händler wieder den gleichen Erwartungswert besitzen. Während des Übergangs von einer vorherrschenden Meinung zu einer anderen kann es vorkommen, daß zwei ungefähr gleichgroße Gruppen von Anlegern um die Vorherrschaft kämpfen. In einem solchen Fall kann nicht gesagt werden, welche Meinung sich letztendlich durchsetzen wird. In den Kursen wird dieser "Kampf" durch schwankende Kurse erkennbar, wobei es jeweils eine Ober- und Untergrenze gibt, die nicht überschritten wird. Kommt es letztendlich zu einem Ausbruch aus diesem Bereich, so setzt sich die überhandnehmende Meinung i.a. ziemlich rasch durch.
Die obige Abbildung zeigt den Erwartungswert eines Aktienkurses in Abhängigkeit von der vorherrschenden Meinung, dargestellt als Wahrscheinlichkeitsverteilung. In Bild 1 haben alle Händler den gleichen Erwartungswert und die gleiche Standardabweichung für den Aktienkurs (37). Bild 2 bis Bild 4 zeigt die Änderung der Verteilung im Zeitablauf, wobei ein Übergang von einer unimodalen zu einer bimodalen Wahrscheinlichkeitsverteilung erfolgt (38). Dies stellt nur ein Fall in der von Vaga entwickelten Kapitalmarkttheorie dar. Ganz allgemein konstruiert diese als "Coherent Market Hypothesis" (CMH) bezeichnete Theorie ein dynamisches, statistisches Modell eines Kapitalmarktes, wobei dieses Modell aus einer Kritik am CAPM entstanden ist: auf realen Aktienmärkten sind verschiedene Effekte wie z.B. der Januareffekt nicht mit der Annahme, daß die Aktienkurse einem Random Walk folgen zu vereinbaren. Die CMH schließt das CAPM allerdings als einen Spezialfall mit ein. Dieser Spezialfall wird in Bild 1 dargestellt: die Aktienkurse, bzw. die Renditen sind durch eine Normalverteilung mit einer Schiefe von Null darstellbar. Eine höhere Rendite ist mit einem höheren Risiko verbunden. Durch die Dynamik des Systems kann sich die Verteilung im Zeitablauf ändern, wodurch 4 grobe Unterscheidungen getroffen werden können. Eine Normalverteilung mit einer Schiefe von Null bedeutet daß die Kurse zufällig sind, und es sich um einen effizienten Markt handelt. Für den Anleger bedeutet dies eine geringe Rendite bei geringem Risiko. Im Fall 2 ist die Verteilung rechtsschief, d.h. bei geringem Risiko wird eine hohe Rendite erreicht (Coherend Bull). Im dritten Fall ist die Verteilung linksschief, wodurch bei geringem Risiko eine negative Rendite erzielt wird (Coherent Bear). Der letzte Fall ist der eines chaotischen Marktes: für den Anleger bedeutet das eine hohes Risiko bei einer geringen Rendite. Der Übergang von Fall 1 zu Fall 4 ist durch die Bilder 1 bis 4 dargestellt. Die Fälle 2 und 3 sind nicht abgebildet.
Ökonomisch läßt sich Bild 4 als der oben erwähnte Fall eines Aktienmarktes mit schwankenden Kursen beschreiben: zwei gleich große Anlegergruppen besitzen jeweils verschiedene Erwartungen. In der Chartanalyse ist eine solche Konstellation durch ein Rechteck gegeben, wobei der obere Erwartungswert eine Widerstandslinie und der untere Erwartungswert eine Unterstützungslinie darstellt. Ein Chartist interpretiert, wie bereits erwähnt, diese Konstellation als Unsicherheitssituation; es kann keine Aussage darüber gemacht werden, in welche Richtung sich die Aktienkurse tatsächlich bewegen werden, sobald sie aus der Formation ausbrechen. Obwohl die Chartisten nicht mit konkurrierenden Anlegergruppen argumentieren, erkennen sie genau die Eigenschaften des obigen Modells. Welche der beiden gleich starken Anlegergruppen schlußendlich überwiegen wird, kann weder der Chartist noch das obige Modell prognostizieren.
Dieses letztes Kapitel stellt einen kleinen Ausblick dar und bietet dadurch Raum für weitere Forschungen. Das Neue, das hier versucht wurde, ist eine Verbindung zwischen theoretischen Ansätzen zur Modellierung eines Kapitalmarktes aus dem großen Bereich der Chaostheorie und der experimentellen Ökonomie herzustellen. Auf diese Verbindung konnte allerdings nur hingewiesen werden, dies nicht zuletzt, da der APSM nicht für solche Fragestellungen designed wurde. Es ist mir ganz klar, daß die Ausführungen zum Thema "chaotische Märkte" mehr Fragen als Anworten aufgeworfen haben (39). Das große Problem jener, die sich mit der Untersuchung von chaotischem Verhalten am Kapitalmarkt beschäftigen, ist zum einen das Problem der Datenmenge; nur Zeitreihen über Jahrzehnte liefern i.a. genügend Daten für eine entsprechende Untersuchung. Zu beachten ist in diesem Zusammenhang, daß detailiertere Daten, wie z.B. anstatt eines Kurses pro Tag einen Kurs alle zehn Minuten zu verwenden, die Datenreihe für Untersuchungen nicht unbedingt geeigneter machen (40). Zudem liegt das Problem bei den Daten an sich. Die CMH besagt ja, daß zu verschieden Zeitpunkten verschiedene Situationen am Markt herrschen. Wie kann ich allerdings unterscheiden, von wann bis wann z.B. ein Coherent Bull dauert (41)? Alle bisherigen Forschungen begnügten sich deshalb mit der Auswertung der Gesamtdaten, was bedeutet, daß nur der Markt im Durchschnitt untersucht wird. Eine Lösung dieser Probleme ist (noch) nicht in Sicht. Ich kann mir allerdings gut vorstellen, daß hier die experimentelle Ökonomie gute Ansatzpunkte liefern könnte. Ähnlich wie die Entwicklung von ganz einfachen mündlich durchgeführten Experimenten bis hin zu Feldexperimenten wie den APSM, um verschiedene Fragestellungen wie z.B. die Hayek-Hypothese, das Auftreten von Price-Bubbles oder die Prognose des Ausgangs von politischen Wahlen zu überprüfen, so wäre z.B. die Frage wann sich ein Markt chaotisch verhält und wann nicht, eine Herausforderung für die experimentelle Ökonomie.
Neben weiterführenden Studien scheint es aber auf jeden Fall angebracht zu sein, etablierten Experimenten, wie z.B. den in dieser Arbeit beschriebenen politischen Aktienmärkten, weiterhin entsprechende Aufmerksamkeit zu schenken. Die Erfolge der letzten Jahre machten, wie auch der APSM zeigen konnte, politische Aktienmärkte zu einem Werkzeug, das den traditionellen Methoden der Meinungsforschung zumindest ebenbürtig ist.
 Voriges Unterkapitel 3.6
Voriges Unterkapitel 3.6
 Einleitung
Einleitung
 Experimentelle Ökonomie
Experimentelle Ökonomie
 Austrian Political Stock Market
Austrian Political Stock Market
 Literaturverzeichnis
Literaturverzeichnis
 Inhaltsverzeichnis
Inhaltsverzeichnis
 Zur ASPM-Homepage
Zur ASPM-Homepage
Page Design: strauss@ebweb.tuwien.ac.at
Last Update: 27.11.1995